Dato per acquisito il fatto che i meccanismi collisionali sono stati
determinanti per l'evoluzione fisica e dinamica degli asteroidi, è logico ipotizzare la
possibilità di identificare, attraverso analisi dinamiche, quali corpi si possano essere
formati in seguito ad un impatto, ricostruendo in tal modo vere e proprie famiglie di
oggetti riconducibili ad una origine comune.
L'ipotesi di fondo è che tali oggetti possano essere riconosciuti grazie al fatto di
presentare elementi orbitali molto simili, proprio in forza del comune luogo di
formazione.
Tale ipotesi fu in qualche modo verificata già nel 1918 dal giapponese Hirayama, il
quale, diagrammando le caratteristiche orbitali (semiasse, eccentricità e inclinazione)
degli asteroidi, notò l'esistenza di ben definiti addensamenti di oggetti, e questa
situazione lo portò ad introdurre il concetto di famiglie dinamiche. Tali
addensamenti sono ben visibili nella figura, che riporta il diagramma sin i - a per oltre
12.000 asteroidi; nella stessa figura si possono individuare anche le lacune
corrispondenti a zone di risonanza (Figura 4 - Zappalà e Cellino, Asteroid
Families, 1993).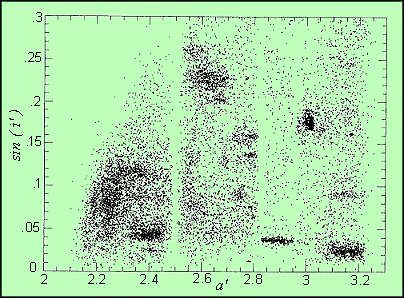
In sostanza si tratta di oggetti non fisicamente vicini nello spazio, ma caratterizzati
da parametri orbitali originari (detti elementi propri) molto simili, e ciò viene
collegato ad un'origine comune; di alcune di queste famiglie è anche stata tentata una
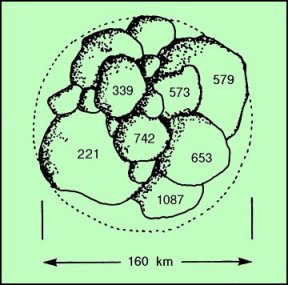
probabile ricostruzione. Nella ricostruzione della famiglia di Eos (Figura 5 - Lang
e Whitney, Vagabondi nello spazio, 1994) si riconoscono: 221 Eos, 339 Dorothea, 573
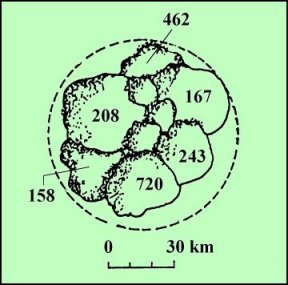
Recha, 579 Sidonia,. 653 Berenike, 742 Edisona e 1087 Nata. In quella successiva, che
riporta la ricostruzione della famiglia di Koronis, (Figura 6 - Lamberti, l'astronomia,
138, 6; 1993) si riconoscono 158 Koronis, 167 Urda, 208 Lacrimosa, 243 Ida, 462
Eriphyla e 720 Bohlina.
Il termine famiglia ha in sè una duplice possibile valenza: dal
punto di vista dinamico indica un gruppo di asteroidi dotati di elementi propri molto
simili, dal punto di vista fisico va correlato ad una origine comune, indicando
pertanto un insieme di frammenti provenienti dalla distruzione di un corpo progenitore.
Non necessariamente, però, questi due significati devono coincidere, è questo il motivo
per cui sono state proposte anche nomenclature alternative (quali clan, cluster...)
riservando il termine famiglia solo per gli asteroidi per i quali coincidono le analisi
fisiche e quelle dinamiche.
Indirizzando la nostra attenzione sulla classificazione dinamica, possiamo rilevare che la
determinazione del numero delle famiglie e l'identificazione degli asteroidi ad esse
appartenenti è un problema affrontato, dopo Hirayama, da molti ricercatori con differenti
risultati.
Dall'introduzione del concetto di famiglia dinamica fino all'inizio degli anni '80 sono
state introdotte sette classificazioni.
Alcune caratteristiche sono riassunte nella seguente tabella:
Autore |
Anno |
N. oggetti |
N. famiglie |
| Hirayama |
1918/1933 |
1223 |
9 |
| Brouwer |
1951 |
1563 |
18 |
| Arnold |
1969 |
1735 |
37 |
| Lindblad e Southworth |
1971 |
1735 |
|
| Carusi e Massaro |
1978 |
1861 |
10 |
| Kozai |
1979 |
2125 |
72 |
| Williams |
1979 |
1796 |
104 |
Le differenze tra queste classificazioni vengono analizzate da Carusi e Valsecchi
(1982) e ricondotte a 5 possibili fattori:
1. metodo utilizzato per il calcolo degli elementi propri; con questo
termine si intendono i parametri orbitali calcolati rimuovendo gli effetti delle
perturbazioni indotte dai pianeti (effetti gravitazionali e di risonanza);
2. criterio di accettazione degli oggetti da classificare;
3. dimensioni numeriche del campione a disposizione;
4. metodi utilizzati per l'identificazione delle varie famiglie;
5. criterio di esclusione o accettazione dei singoli asteroidi come
membri di una famiglia (evidentemente legato strettamente al metodo di identificazione
utilizzato).
Dal lavoro citato emerge un sostanziale accordo su quelle famiglie che, usando il
termine nel senso più stretto, possono essere definite famiglie di Hirayama (in
quanto indicate come tali dall'astronomo giapponese nel 1933), vale a dire: Themis, Eos,
Koronis, Maria (ex Egeria) e Flora.
Ad esse si possono affiancare Phocaea e Nysa, non considerate da Hirayama, ma identificate
dagli altri ricercatori.
Riguardo alle altre famiglie emerge un quadro molto variegato nel quale per alcuni casi si
possono notare sostanziali accordi, mentre per altri esistono anche notevoli diversità
tra le classificazioni.
Un aumento di interesse e di motivazione si è avuto verso la fine degli anni 80; ad esso
hanno contribuito molti fattori, ma forse quelli decisivi possono essere identificati
(Zappalà et al., 1990) nei seguenti:
a) approfondimento degli studi dinamici sulle orbite degli asteroidi, soprattutto per
quanto riguarda i meccanismi di risonanza, e dunque maggiore affidabilità nella
determinazione degli elementi propri;
b) aumento notevole delle informazioni sulle tipologie tassonomiche e sui dati fisici
(dimensioni, profili, ...) degli asteroidi, e dunque possibilità di approfondire le
analisi sulle singole famiglie;
c) nuovi modelli collisionali in grado di offrire una controparte teorica alla situazione
descritta attraverso le famiglie dinamiche, ormai accettate come risultato di impatti
asteroidali molto violenti.
Una fondamentale innovazione è stata l'introduzione dell'idea che si potesse
realizzare una classificazione di famiglie dinamiche per mezzo di procedure interamente
automatiche, dunque basate su criteri oggettivi.
Uno di questi metodi (Zappalà et al., 1990) è chiamato hierarchical clustering e
consiste (in una descrizione sommaria) nell'applicazione dei seguenti passi:
1. i dati di riferimento utilizzati sono gli elementi propri (a', e',
sin i') del campione di asteroidi preso in considerazione;
2. viene definita, nello spazio tridimensionale degli elementi propri,
una metrica che consenta di determinare le distanze tra gli elementi di questo spazio;
3. si determinano i raggruppamenti esistenti calcolando le mutue
distanze (v) tra gli elementi dello spazio, ed in base a queste si costruisce un
diagramma a stalattite (v-N);
4. si deve a questo punto individuare quale raggruppamento costituisca
una possibile famiglia dinamica e quale, invece, sia frutto di un addensamento casuale; in
altre parole si tratta di determinare quale sia il valore di soglia al quale
"tagliare la stalattite".
Naturalmente quest'ultimo passo non è frutto di scelte arbitrarie, ma proviene
dall'introduzione di una popolazione asteroidale fittizia (e casuale) la cui distribuzione
fornisce i valori di soglia cercati.
L'introduzione di criteri oggettivi nella determinazione delle famiglie dinamiche ha
comportato un'ulteriore crescita di interesse e nuovi studi.
Molto importante l'analisi (Zappalà et al., 1995) effettuata su una popolazione di 12.487
asteroidi attraverso due differenti tecniche di clustering (hierarchical clustering
e wavelet analysis, quest'ultimo basato sul concetto di densità nello spazio degli
elementi propri) i cui risultati sono poi stati comparati.
Per fare il punto sulla attuale situazione in merito alle conoscenze relative alle
famiglie dinamiche, ritengo sia fondamentale riportare proprio i risultati ottenuti nello
studio appena citato.
Gli asteroidi del campione considerato (7.871 dei quali non hanno numerazione) sono stati
suddivisi in tre gruppi in base alla posizione occupata nella Fascia Principale; le
caratteristiche di questa suddivisione possono essere riassunte in questo schema:
| |
ZONA INTERNA |
ZONA INTERMEDIA |
ZONA ESTERNA |
| a min (UA) |
2.065 |
2.501 |
2.825 |
| a max (UA) |
2.501 |
2.825 |
3.278 |
| N TOT |
5451 |
3711 |
3325 |
| N NUM |
1691 |
1274 |
1651 |
Le tabelle seguenti riassumono, per ciascuna zona, la situazione delle famiglie
identificate come tali da ambedue i metodi di clustering.
In ogni tabella viene riportato il nome identificativo di ciascuna famiglia (a
volte differisce tra i due metodi), il numero di oggetti individuato come
appartenente alla famiglia da ciascuna delle due tecniche (HCM = hierarchical clustering
method, WAM = wavelet analysis method) ed infine il numero di oggetti comuni ai due
gruppi.
TABELLA I - Zona Interna
Id (HCM) |
NHCM |
Id (WAM) |
N
WAM |
N
COM |
| 8 Flora |
604 |
43 Ariadne |
575 |
434 |
| 44 Nysa |
381 |
35 Hertha |
374 |
300 |
| 4 Vesta |
231 |
4 Vesta |
242 |
187 |
| 20 Massalia |
49 |
20 Massalia |
45 |
33 |
| 163 Erigone |
45 |
163 Erigone |
49 |
42 |
TABELLA II - Zona Intermedia
| Id(HCM) |
NHCM |
Id(WAM) |
NWAM |
NCOM |
| 15 Eunomia |
439 |
15 Eunomia |
303 |
298 |
| 1 Ceres |
89 |
93 Minerva |
88 |
84 |
| 170 Maria |
77 |
170 Maria |
83 |
74 |
| 668 Dora |
77 |
668 Dora |
79 |
75 |
| 145 Adeona |
63 |
145 Adeona |
67 |
61 |
| 125 Liberatrix |
44 |
847 Agnia |
74 |
35 |
| 110Lydia |
26 |
110Lydia |
50 |
26 |
| 808 Merxia |
26 |
808 Merxia |
29 |
26 |
| 569 Misa |
25 |
569 Misa |
27 |
23 |
| 1726 Hoffmeister |
22 |
110 Lydia |
50 |
15 |
| 1726 Hoffmeister |
22 |
272 Antonia |
12 |
7 |
| 2085 Henan |
22 |
847 Agnia |
74 |
19 |
| 410 Chloris |
21 |
410 Chloris |
27 |
21 |
| 1644 Rafita |
21 |
1644 Rafita |
23 |
21 |
| 128 Nemesis |
20 |
58 Concordia |
38 |
20 |
| 1128 Astrid |
10 |
1128 Astrid |
11 |
10 |
| 1639 Bower |
10 |
342 Endymion |
15 |
10 |
TABELLA III - Zona Esterna
| Id
(HCM) |
N
HCM |
Id
(WAM) |
N
WAM |
N
COM |
| 24 Themis |
550 |
24 Themis |
517 |
491 |
| 221 Eos |
477 |
221 Eos |
482 |
444 |
| 158 Koronis |
325 |
158 Koronis |
299 |
289 |
| 10 Hygiea |
103 |
10 Hygiea |
175 |
97 |
| 490 Veritas |
22 |
92 Undina |
36 |
22 |
| 137 Meliboea |
13 |
137 Meliboea |
16 |
13 |
| 1298 Nocturna |
18 |
10 Hygiea |
175 |
18 |
| 293 Brasilia |
10 |
293 Brasilia |
18 |
10 |
Si può notare un sostanziale accordo tra i due metodi,
almeno per quanto riguarda le famiglie più numerose ed importanti, ma sono evidenti anche
notevoli differenze (piccoli gruppi identificati come famiglie da un metodo e non
classificati in modo così sicuro con l'altro, raggruppamenti confinanti riuniti da una
tecnica e non dall'altra, ecc...). Queste differenze non fanno che confermare come
non sia possibile stilare una lista delle famiglie limitandosi ad impiegare le analisi dei
soli parametri dinamici, ma queste devono essere sostenute e avvalorate da altre indagini
(spettrofotometria, dimensioni, albedo, ecc.), cioè si deve confermare una omogeneità di
parametri fisici che possano testimoniare l'origine comune.
In questa direzione si può collocare la recente survey spettroscopica dei piccoli
asteroidi della Fascia Principale (Shui Xu et al., 1995) che non solo ha chiaramente
mostrato per alcune famiglie l'omogeneità tassonomica degli asteroidi ad esse
appartenenti, ma ha anche evidenziato, per altre, una notevole varietà di tipologie.
Questa conclusione, se da un lato sottolinea una volta di più la problematicità talvolta
presente nell'identificazione delle famiglie, dall'altro rende merito, se ancora fosse
necessario, alla felice intuizione di Hirayama.
Emerge inoltre la fondamentale e pressante esigenza di costruire modelli evolutivi teorici
che siano in grado di fornire situazioni dinamiche in linea con le attuali conoscenze
della distribuzione spaziale e dimensionale degli asteroidi.
|